And that is my answer to people who complain i use CD's to decode over LP's whenever i can, especially classical - i thank EMI for having gone single inventory for so many years.
On a different point, i've started to hate SQ. yes, you heard it right. I used to think QS was the pits, but now (from a decoding point of view) QS is better to deal with.
I'd be really interested in seeing some test info using the SQT1100 test LP through various decoders (preferbly not the tate as i suspect it's good at hiding the problems).
Things like:
Phase response
Chan ID (decoded)
There's a basic problem with SQ is, if you forget about the phase encoding, is that the rears are actually MONO!
If in doubt, here's the basic SQ encoding equation:
Lt = Lf + (0.707 Lb -j) + (0.707 Rb)
Rt = Rf + (-0.707 Lb) + (0.707 R +j)
The problem comes in "decoding" the rears back to stereo. It causes serious phase shifts, which are impossible to correct. This is what i'm up against, and am now in the situation where i have to either keep the Rear Center in phase, but the Rear L & R's seriously out of phase, or bring the L & R's back "nearer-ish" where they should be and have the Rear Center out of phase.
It doesn't matter how you attempt it, it always ends up the same. Sigh...
You don't get this problem with QS
You're only looking at the encode equations (it seems to me). Taking it through the full decode produces full stereo fronts and rears with in-phase center front and center back.
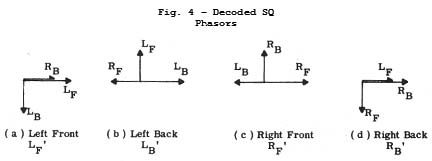
Look at the decoded phasors of SQ with a basic matrix (non-blend) decoder - the rears are full stereo and in phase with each other due to the subtraction from each other in the basic decode and center back (which isn't shown - neither is CF) is in phase too. There's just no front to rear separation (or virtually none). The Automatic dimension control patent, the Synthesis of 4-2-4 Matrix Systems paper and the MCS Review reply go into more detail, with the MCS review showing the Energy Sphere for SQ and that the rears are true stereo (since they are 180 degrees apart on the sphere) and CB in phase. The 4-2-4 Matrix Systems Interchangeability paper by John Eargle on my site is also an excellent read regarding SQ (although it deals with only the original 'square' SQ encoder) and also shows the Energy Sphere for the different systems.
There's no Left Back in Right Back and vise-versa.
There are several (3) versions of QS, I'll try to post the papers - I have one on my site about QS encoding and Vario-Matrix decoding.
I think the problems your running up against with the PC decoding is that the encoding process is 'adaptive' meaning different channels changing dominance as the music changes and therefore, the decoding must be adaptive too, changing the decoders structure as a function of the music.
Martin Willcocks "Surround Sound In the 80's Advances in Decoder Technology" explains it in great detail, but it's a huge 27 page scan that I just haven't gotten the gumption to scan and turn into a PDF for uploading yet. Here's a OCR scan of some of it without the graphics - I tried to keep the equation formatting as correct as possible:
_________
We can consider a surround sound master tape (any number of channels) as a vector signal
s(t) having one component for each tape track (a similar requirement applies to any discrete number of source signals). Thus,
s(t) = (s[SUB]1[/SUB] (t), s[SUB]2[/SUB](t), s[SUB]3[/SUB](t), s[SUB]4[/SUB](t))
for a four-track master. Each of the signals is a distinct real function of time, but may be considered as analytic signals having an imaginary part which is equal to the Hilbert transform of its real part. The composite signal is treated as a column vector function of time. It is an element of the source signals vector space spanned by the basis vectors corresponding to unity signals in each of the input channels.
The matrix encoding process is represented by a complex matrix
E which is generally time-invariant, although exceptions are possible. The transformation has both real and imaginary components, and since it typically encodes four channels into two, it is a complex matrix of dimension 2x4. The imaginary-valued coefficients of this matrix are physically realized by pairs of all-pass phase-shifting networks having a phase difference at all audio frequencies of 90º degrees (within acceptable tolerance limits), one pair for each input channel, the outputs representing the real and imaginary parts of the input signals . It is then a simple matter to apply appropriate gains representing the encoder coefficients and sum the outputs into the various output channels. These pairs of all-pass quadrature networks often occur in audio and communications circuitry where they perform the function of a Hilbert Transformer, or they may be implemented via digital DSP code. An ideal Hilbert Transformer is physically unrealizable.
Representing the encoder output signals as another complex vector function of time,
e(t) = (e[SUB]1[/SUB](t), e[SUB]2[/SUB](t)), we can write the encoding equation as:
e(t) = E s(t)
By similar reasoning, the simple fixed matrix decoder can be represented by another complex matrix
D of dimension 4x2, and the decoding equation becomes.
d(t) = D e(t)
Ideally, one would like to have the decoded signals vector represent, as clearly as possible, the input signals to the encoder, if we are considering a matrix system of the kind represented by SQ or QS, where the input signals are “discrete 4-channel”, representing speaker feeds at the four corner locations, and the decoded signals are also intended to be speaker feeds for the same locations in the listening room. This implies that the product of the encoding and decoding matrices should be
I[SUB]4[/SUB], the complex identity matrix of dimension 4x4, i.e. we would like to satisfy:
D E = I[SUB]4[/SUB]
This is, of course, mathematically and physically impossible, since both
D and
E have rank 2, and their product must be a 4x4 matrix of rank 2. In other papers it has been shown that the best decoder is represented by the pseudo-inverse of the encoding matrix. Such a decoder is known as a “matched decoder”, and has the property that:
E D = I[SUB]2[/SUB]
Where
I[SUB]2[/SUB] is the 2x2 complex identity matrix. We should note at this point that the decoded signals vector is an element of the decoded signals vector space
D which is isomorphous with the source signals vector space
S.
2.2 ADAPTIVE DECODING
Using this approach, the solution to the decoding problem at once becomes clear. Since the source signals are time-varying functions, the decoded signals are also time-varying, and contain various proportions of the source signals in the different channels. We define the overall transformation matrix
T as a 4x4 complex matrix which is the product of the encoding and decoding transformations,
T = D E
Our aim is, at all times, to make
T come as close to
I[SUB]4[/SUB] as possible. One way to do this is to directly vary the coefficients of
D as a function of information derived from the relative phases and amplitudes of the encoded signals. This is the approach taken in the Sansui QS Vario-Matrix decoder, although the decoder was not formulated this way. Another way to do it is to multiply the decoder output signals vector
d(t) by another transformation matrix
M(Ø), where
Ø is a parameter representing the direction of the predominant source signal present at any time. This is the approach taken in the Directional Enhancement System. The matrix
M(Ø) is called the modifying matrix, and its product with
d(t) is the modified decoded signals vector
m(t). Thus, the Directional Enhancement System is represented by the single equation:
m(t) = M(Ø(t)) d(t)
since
Ø is also a time-varying parameter. Then, the overall transformation matrix for azimuth
Ø is given by
T[SUB]Ø[/SUB] = M[SUB]Ø[/SUB] D E
And, as the predominant azimuth varies, the complete encode-decode-modify process is represented by:
T(Ø) = M(Ø) D E
Of course, many other types of surround sound decoder can also be represented this way, but the Directional Enhancement System was derived from this analysis, not the other way around. This system as formulated contains a means for determining the value of
Ø as a function of the input signals, a means for computing the appropriate values of the coefficients of
M(Ø), and a matrix multiplier circuit which performs the multiplication of the decoded signals by the modifying matrix thus derived.
One way in which
M(Ø) can be computed is to represent it as a linear combination of different matrices for different directions. It is not hard to compute the correct form for
M(Ø) for any specific azimuth
Ø from the ideal encoding for
Ø on the assumption that the output of the DES,
m(t) should be equivalent to the Pair-Wise-Mixed (PWM) input to the encoder corresponding to
Ø. This is especially true if the six principle directions for the SQ code, which correspond to the positive and negative X, Y, and Z axes of the energy sphere, are chosen, i.e. the directions CF (0º), CB (180º), LB (225º), RB (135º), RF (45º), and LF (315º). Representing the modifying matrix for azimuth angle
Ø by using
Ø as a subscript, we can compute the six matrices (fig.-) for these principle directions quite easily. Then the form for
M(Ø) is:
M(Ø) = S[SUB]Ø [/SUB]C[SUB]Ø [/SUB]M[SUB]Ø + [/SUB](1 - S C[SUB]Ø[/SUB]) [SUB]Ø[/SUB] I[SUB]4[/SUB]
where the
C[SUB]Ø[/SUB] are the directional control factors for the corresponding modifying matrices, and may take values between 0 and 1. If all the
C[SUB]Ø[/SUB] are zero, the modifying matrix will become the identity matrix
I[SUB]4[/SUB], so that simple matrix decoded signals pass through the system unchanged to the output amplifiers and loudspeakers. Hence we can consider the modifying matrix to be the sum of the identity matrix and a direction-dependent matrix, which we shall define as
B[SUB]Ø[/SUB].
The coefficients of the
B[SUB]Ø[/SUB] matrices are fixed, and the direction control signals can be determined from the input signals by a direction detection system.
In the DES, the direction detection system works by first normalizing all four input signals from the matrix decoder
D using an AGC loop. These signals are matrixed, full-wave rectified, smoothed, and summed to give a reference signal which is set at a suitable level relative to the smoothed outputs and is also used by the AGC loop, and fed to non-linear amplifiers where they are compared with the reference signal. The outputs of these amplifiers are always zero if the input from the rectifier is greater than the reference, but increases linearly to a voltage representing unity coefficient factor as the rectifier output falls from the reference level to just above zero, then limits at unity level as the rectifier output falls from this level to zero.
The proper choice of reference level is that which ensures that no more than two of the rectifier outputs will fall below it when any ideally encoded signal corresponding to a single sound source at any horizontal azimuth is applied to the decoder input preceding the DES. The correct choice of gain for the linear region of the comparison amplifiers is the gain which will generate outputs from the appropriate comparison amplifiers each equal to half the maximum output when an optimally SQ encoded Center Left signal is presented to the decoder, so that the direction control signals, which are the outputs of the comparison amplifiers, are as given in equation (47) of the patent:
B[SUB]270[/SUB] = 0.5 B[SUB]225[/SUB] + 0.5 B[SUB]315[/SUB]
Which ensures correct decoding of the Center Left signal. Similar results then occur for Center Right and both diagonal splits. It turns out that the sum of the direction control signals is not exactly unity for all possible inputs to the decoder using this directional detection scheme, and additional limiting circuitry, and subject to a separately granted patent, is used to prevent this sum from exceeding unity. This helps to ensure smooth operation of the decoder on a dynamic basis.
The coefficients
b[SUB]Ø[/SUB] of the
B(Ø) matrix can be implemented in practice by signal combiners in which the control signals
C[SUB]Ø[/SUB] are applied as inputs and multiplied by fixed coefficients corresponding to those for each principal direction, then summed to yield the coefficient signals. These in turn are applied to the matrix multiplier section, where the input signals are also added to the matrix product to implement equation (13)
The DES, designed according to the above principles, works very well for static conditions; continuous sinewave inputs corresponding to any azimuth are decoded with near-perfect separation (35-50 db depending on direction). The dynamics of the system are very complex, and require great care to establish the correct attack and decay times for the direction control signals and behavior when complex events occur in the music. In the last commercial implementation of the decoder, the Fosgate Research Tate II 101A Surround Stereo Decoder, much research was required to fine-tune these dynamic characteristics, and Jim Fosgate deserves recognition for his work on these aspects of the DES performance, which were incorporated into an interface circuit external to the IC’s..
Because the DES is capable of recognizing roughly equal signals in each of the X, Y and Z directions of the energy sphere simultaneously, and provides a modifying matrix which increases separation for all the simultaneous signals, it has essentially a three-axis control system (all other adaptive decoders, either before or since, are two-axis and can increase separation for only one direction at a time). The consequence of this is that the DES is hardly ever reduced to the level of a simple fixed matrix decoder, even in complex musical situations, and a very open and spacious decoding effect is the result, with no observable phasiness. Phantom Center Front images are precisely in phase, as are all stereo images across the front stage, so that mislocation and spreading of these images due to relative broadband phase shifts does not occur.